Does the Concentration of Airborne Lead Affect the Number of Complaints due to Lead in NYC?
Hypothesis
My hypothesis is that when there are changes in the concentration of lead in the NYC air, there will also be correlated changes in the number of complaints due to lead in the NYC 311 complaints.
About the datasets
The 311 dataset comes from the NYC open data website that can be found here: ‘NYC 311’. The data on the air quality came from the EPA website here: ‘EPA’.
Choosing complaints
There are a number of different complaints in the NYC 311 dataset. I have chosen complaints that I think will show any direct correlation. Specifally I focus on complaints that could be due to lead contaminants in water, lead in paint, and lead in waste.
complaints <- c('Lead','Radioactive Material','Water Quality',
'Air Quality','Industrial Waste','Drinking Water',
'Water System','Drinking','PAINT/PLASTER',
'PLUMBING', 'General Construction/Plumbing')
filtered_df <- df_311 %>% filter(`Complaint Type` %in% complaints) %>%
select(date_ = Date, `Complaint Type`, Longitude, Latitude)
dim(filtered_df)[1] 139413 4We can see that there is over 139,000 observations
During other anlyses of the PM2.5, carbon monoxide, and ozone air quality datasets, the air quality index (AQI), was a good indicator for those variables.
If we look at the unique values we can see that they do not vary at all so would not be helpful in any analyses.
unique(df_pb$DAILY_AQI_VALUE)[1] 0unique(df_pb$DAILY_OBS_COUNT)[1] 1In this case we will just use the concentraion of lead in the air as our independent variable.
Next we will check for duplicates in the dates. Duplicates may occur from air quality measuremnts taken on the same day, from different measurement stations. We will take the mean of them all.
sum(duplicated(df_pb2$date_))[1] 235df_pb3 <- df_pb2 %>% group_by(date_) %>% dplyr::summarise(Pb.conc = mean(Pb.conc))
head(df_pb3)Source: local data frame [6 x 2]
date_ Pb.conc
(date) (dbl)
1 2015-01-06 0.0040
2 2015-01-12 0.0048
3 2015-01-18 0.0028
4 2015-01-24 0.0038
5 2015-01-30 0.0100
6 2015-02-05 0.0156There are indeed duplicates in the date, and moreover we can see data is taken every 6 days.
We can plot the variation in lead concentration in \(\frac{\mu g}{m^3}\) over time.
We can plot the location of the measurement station in the NYC area, and that there is only one. Because of this we will only take data in the boroughs closest to the measurement station, Manhattan, Staten Island, and Brooklyn, as this will most closely represent the lead concentration from at the location of the complaints. Moreover we will only use the lead concentration from this measurement station.
We can also look at the location of the complaints in NYC. We can see that they are pretty spread out over the boroughs chosen and we cannot see any clear trend.
Because we only want to work with one table we will inner join the two tables.
We summarise the data via the complaint type because we want to see whether the complaints about ‘Lead’ are dependent on the air concentration of lead.
df_tot2 <- df_tot %>% dplyr::group_by(date_, `Complaint Type`) %>%
dplyr::mutate(total.counts = n()) %>% ungroup()Before we do any statistics we split dataset into a testing and training dataset. To confirm any hypotheses we perform on the training set we also perform on the test dataset.
set.seed(3456)
trainIndex <- createDataPartition(df_tot2$total.counts, p = .8, list = F)
df_tot_train <- df_tot2[ trainIndex,]
df_tot_test <- df_tot2[-trainIndex,]We also split the training dataset into those complaining due to ‘Lead’ complaints, and those otherwise.
df1_t <- df_tot_train %>%
filter(`Complaint Type` == 'Lead') %>%
select(total.counts, Pb.conc) %>%
na.omit()
df2_t <- df_tot_test %>%
filter(`Complaint Type` != 'Lead') %>%
select(total.counts, Pb.conc) %>%
na.omit()We can now plot the two.
We can see that there is a postive correlation when the complaints are categorized due to ‘Lead’, for the other complaints there is a slight negative correlation. This may indicate that when the air concentration of lead is high there are more ‘lead’ complaints.
To test this hypothesis further we can perform a T-test.
t.test(x = df1_t$total.counts, y = df2_t$total.counts)
Welch Two Sample t-test
data: df1_t$total.counts and df2_t$total.counts
t = -84.981, df = 2546.8, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-112.8810 -107.7892
sample estimates:
mean of x mean of y
10.53165 120.86677 The T-test shows a p-value less than 0.05 so we determine that the trend is statistically significant.
Linear Regression
Univariate Linear Regression
We can try and fit the number of complaints using linear model with respect to the concentration of lead.
FitLm <- lm(data = df_tot_train, total.counts ~ Pb.conc)
summary(FitLm)
Call:
lm(formula = total.counts ~ Pb.conc, data = df_tot_train)
Residuals:
Min 1Q Median 3Q Max
-123.394 -39.457 -8.193 24.955 288.492
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 125.870 1.042 120.775 <2e-16 ***
Pb.conc -738.257 86.469 -8.538 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 70.93 on 16270 degrees of freedom
Multiple R-squared: 0.00446, Adjusted R-squared: 0.004399
F-statistic: 72.89 on 1 and 16270 DF, p-value: < 2.2e-16From the summary of the fit we can see that although the p-value is very small, indicating statistical significance, the \(R^2\) value is very small, showing that it doesn’t fit the data very well. Multivariate regression
Multivariate Linear Regression
We can also produce more complicated models that depend on polynomial dependence of the concentration of lead, and also on the type of complaint.
FitLm2_1 <- lm(data = df_tot_train, total.counts ~ poly(Pb.conc,2)*`Complaint Type`)
summary(FitLm2_1)
Call:
lm(formula = total.counts ~ poly(Pb.conc, 2) * `Complaint Type`,
data = df_tot_train)
Residuals:
Min 1Q Median 3Q Max
-155.011 -31.711 -1.265 22.238 213.373
Coefficients:
Estimate Std. Error
(Intercept) 22.187 1.917
poly(Pb.conc, 2)1 206.806 235.922
poly(Pb.conc, 2)2 24.124 222.755
`Complaint Type`Drinking -18.510 5.662
`Complaint Type`Drinking Water -20.678 25.562
`Complaint Type`Industrial Waste -18.386 5.765
`Complaint Type`Lead -11.792 4.168
`Complaint Type`PAINT/PLASTER 103.489 2.070
`Complaint Type`PLUMBING 79.702 2.113
`Complaint Type`Water Quality -19.204 6.248
`Complaint Type`Water System 123.473 2.072
poly(Pb.conc, 2)1:`Complaint Type`Drinking -258.155 742.151
poly(Pb.conc, 2)2:`Complaint Type`Drinking -1.689 730.139
poly(Pb.conc, 2)1:`Complaint Type`Drinking Water -266.142 3661.956
poly(Pb.conc, 2)2:`Complaint Type`Drinking Water 14.070 2893.898
poly(Pb.conc, 2)1:`Complaint Type`Industrial Waste -202.745 789.645
poly(Pb.conc, 2)2:`Complaint Type`Industrial Waste -68.515 761.399
poly(Pb.conc, 2)1:`Complaint Type`Lead 2.436 533.487
poly(Pb.conc, 2)2:`Complaint Type`Lead -207.799 510.994
poly(Pb.conc, 2)1:`Complaint Type`PAINT/PLASTER 831.586 256.130
poly(Pb.conc, 2)2:`Complaint Type`PAINT/PLASTER -464.629 242.760
poly(Pb.conc, 2)1:`Complaint Type`PLUMBING 1292.117 260.056
poly(Pb.conc, 2)2:`Complaint Type`PLUMBING -730.928 248.227
poly(Pb.conc, 2)1:`Complaint Type`Water Quality -301.349 1578.916
poly(Pb.conc, 2)2:`Complaint Type`Water Quality -128.587 1846.134
poly(Pb.conc, 2)1:`Complaint Type`Water System -3246.911 258.994
poly(Pb.conc, 2)2:`Complaint Type`Water System 2998.825 249.189
t value Pr(>|t|)
(Intercept) 11.571 < 2e-16 ***
poly(Pb.conc, 2)1 0.877 0.38073
poly(Pb.conc, 2)2 0.108 0.91376
`Complaint Type`Drinking -3.269 0.00108 **
`Complaint Type`Drinking Water -0.809 0.41856
`Complaint Type`Industrial Waste -3.189 0.00143 **
`Complaint Type`Lead -2.829 0.00467 **
`Complaint Type`PAINT/PLASTER 49.983 < 2e-16 ***
`Complaint Type`PLUMBING 37.724 < 2e-16 ***
`Complaint Type`Water Quality -3.074 0.00212 **
`Complaint Type`Water System 59.595 < 2e-16 ***
poly(Pb.conc, 2)1:`Complaint Type`Drinking -0.348 0.72796
poly(Pb.conc, 2)2:`Complaint Type`Drinking -0.002 0.99815
poly(Pb.conc, 2)1:`Complaint Type`Drinking Water -0.073 0.94206
poly(Pb.conc, 2)2:`Complaint Type`Drinking Water 0.005 0.99612
poly(Pb.conc, 2)1:`Complaint Type`Industrial Waste -0.257 0.79737
poly(Pb.conc, 2)2:`Complaint Type`Industrial Waste -0.090 0.92830
poly(Pb.conc, 2)1:`Complaint Type`Lead 0.005 0.99636
poly(Pb.conc, 2)2:`Complaint Type`Lead -0.407 0.68427
poly(Pb.conc, 2)1:`Complaint Type`PAINT/PLASTER 3.247 0.00117 **
poly(Pb.conc, 2)2:`Complaint Type`PAINT/PLASTER -1.914 0.05565 .
poly(Pb.conc, 2)1:`Complaint Type`PLUMBING 4.969 6.81e-07 ***
poly(Pb.conc, 2)2:`Complaint Type`PLUMBING -2.945 0.00324 **
poly(Pb.conc, 2)1:`Complaint Type`Water Quality -0.191 0.84864
poly(Pb.conc, 2)2:`Complaint Type`Water Quality -0.070 0.94447
poly(Pb.conc, 2)1:`Complaint Type`Water System -12.537 < 2e-16 ***
poly(Pb.conc, 2)2:`Complaint Type`Water System 12.034 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 56.84 on 16245 degrees of freedom
Multiple R-squared: 0.3616, Adjusted R-squared: 0.3606
F-statistic: 353.9 on 26 and 16245 DF, p-value: < 2.2e-16We can see that there are many combinations of variables, with around 10 that are statistically significant. Aain we have a very small p-value, and we also get a much better \(R^2\) value, showing a better fit on this training dataset.
This is probably not the best fit of the model since it is assuming normal distribution of the observations. From the plots provided by the fit we can see that this is inaccurate. This is shown in the Q-Q plot in which many of the points do not lie on the normal distribution line. Also the fit is not very good as a few of the points have very high leverage, i.e., small changes in the those points will change the fit dramatically. We can also see that there are two clusters which may warrant further exploration if the model was sufficient otherwise.
Though our R2 value was much better this was most likely due to overfitting of the data.
Elastic network
If we want to make a more accurate prediction model we can use an elastic network, which uses a combination of ridge regression and LASSO to produce a robust model, and less prone to overfitting.
mydv <- dummyVars(~ Pb.conc + `Complaint Type`, data = df_tot_train)
data_cor_new_train <- data.frame(predict(mydv, df_tot_train))
data_cor_new_test <- data.frame(predict(mydv, df_tot_test))
enetGrid <- expand.grid(.alpha = seq(0, 1, 0.05), #Alpha between 0 (ridge) to 1 (lasso).
.lambda = seq(0, 10, by = 1))
ctrl <- trainControl(method = "cv", number = 10,
verboseIter = T)
set.seed(1)
enetTune <- train(df_tot_train$total.counts ~ ., data = data_cor_new_train,
method = "glmnet",
tuneGrid = enetGrid,
trControl = ctrl)
plot(enetTune)plot(varImp(enetTune))Here we can see that the most important variable is the concentration of airborne lead, that may further confirm our hypothesis.
We can test our model on the test dataset and calculate the root mean squared error (RMSE).
[1] 62.50926We confirm the RMSE calculated on the test dataset is on the same order compared to the training dataset indicating a good model fit.
Conclusion
Overall, we have found out that there is correlation between the concentration of airborne lead and the number of lead complaints in NYC, moreover the correlation is statistically significant. We also have modelled the total number of complaints given the concentration of lead, and complaint type. We found that multivariate regression did not perform that great, though elastic networks performed much better as a prediction model.
Though we see correlation and can predict quite well, it is importatnt to note that this does not indicate causation. In the spirit of being rigourously skeptical of the data and predictions, one intersting thing I discovered after performing my analysis of NYC complaint vs air quality, was that the EPA performed a time-series observation of the air quality. They show the air quality over time from 1980, which can be found here, and most importantly, they show a 98% decrease, which is huge. Their figure is shown below in which the white line is mean air quality level, the upper bound shows the air quality of the 90th percentile, and the lower bound shows the air quality for the 10th percentile.
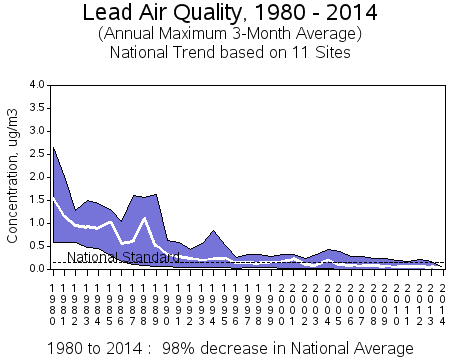
This leads me to believe that there may be some underlying cause, or if there is any causation it is from some hyper-sensitive individuals. I believe this because the air quality levels of lead, even at their peak in past couple years, are negligible compared to their levels in the 80s.