Definition
Recommender systems are a subclass of information filtering system that seek to predict the "rating" or "preference" that a user would give to an item.
For the demonstrative purposes of this post I will be using a dataset of beer reviews from a popular beer rating website. The full python script to accompany this work can be found here, and a link to the dataset can be found here (170Mb).
Resources
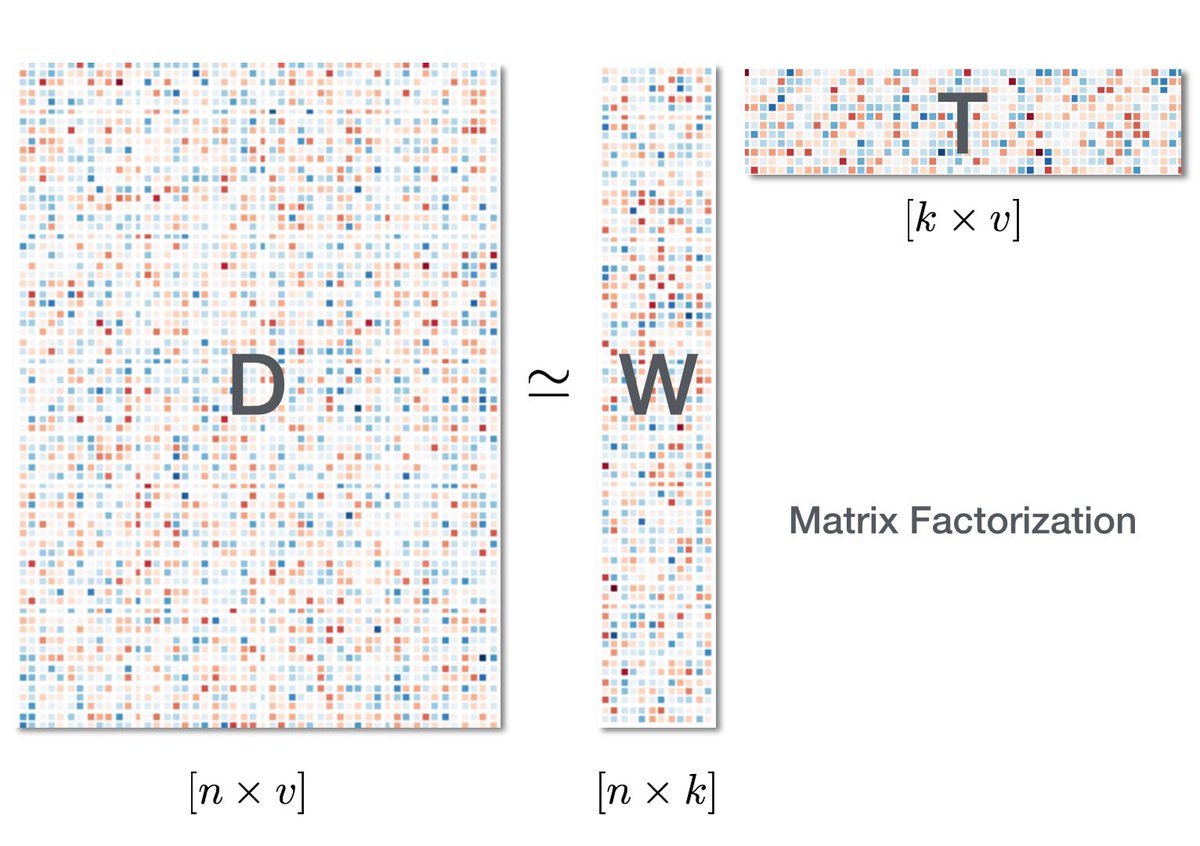
Blog post on matrix factorization by Ethan Rosenthal of Dia & Co.
Jupyter notebook on validating recommendation algoritms on Insight dropbox.
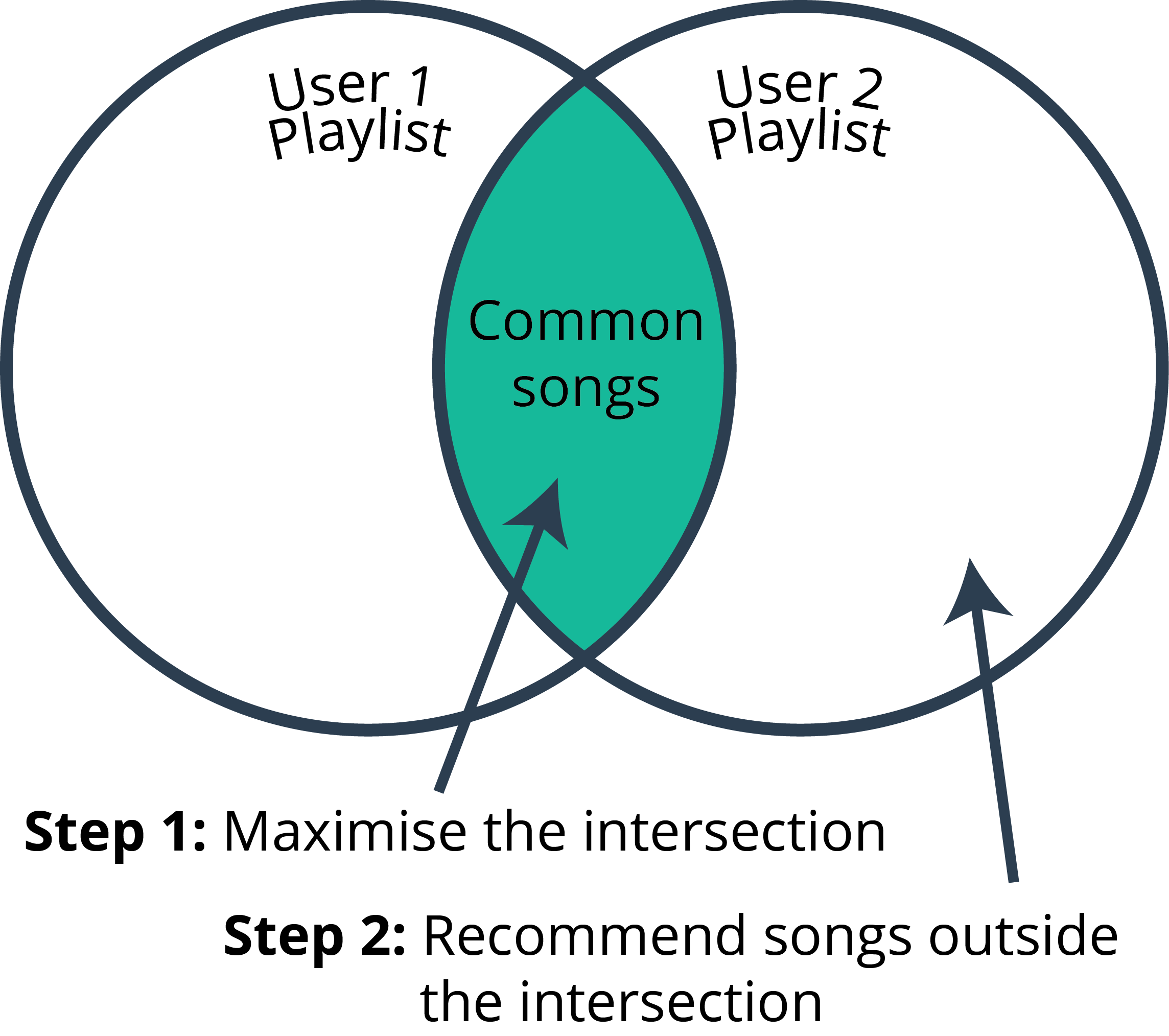
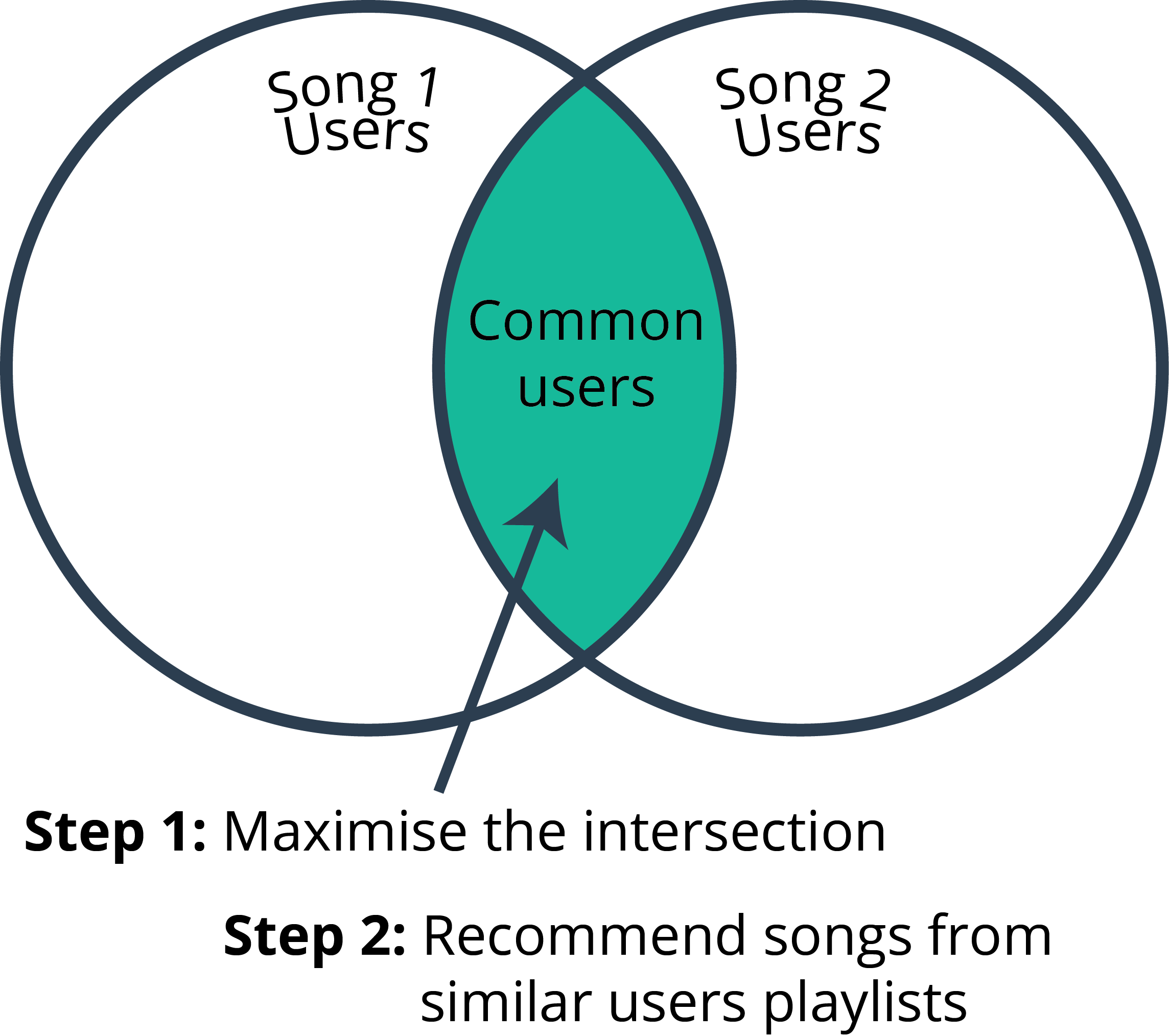
Naïve Solution
Recommend the most popular item. This may be popularity in terms of total number of plays of songs, total number of purchases, or average 5 star ratings.